Розділ 1. Показникова та логарифмічна функції

Вправа 2.66

Розв'яжіть нерівність:
1) 1 + 2х > 9; 2) 6 - 2х ≤ 5; 3) 2 • (3 + х) + (4 - х) ≤ 0;
4) 5(х + 8) + 4 • (1 - х) > 0; 5) 2х² - 3х ≥ 2(x - 1); 6) 4х(х + 2) < 5.

Відповідь:

1) 1 + 2х > 9
2x > 8
x > 4

х є (4; +∞);

2) 6 - 2х ≤ 5
-2x ≤ 5 - 6
-2x ≤ -1 • (-1)
2x ≥ 1
x ≥ 0,5

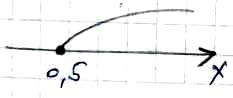
х є [0,5; +∞);

3) 2 • (3 + х) + (4 - х) ≤ 0
6 + 2x + 4 - x ≤ 0
x + 10 ≤ 0
x ≤ -10

х є (-∞; 10];

4) 5(х + 8) + 4 • (1 - х) > 0
5x + 40 + 4 - 4x > 0
x + 44 > 0
x > -44

х є (-44; +∞);

5) 2х² - 3х ≥ 2(x - 1)
2x² - 3x ≥ 2x - 2
2x² - 3x - 2x + 2 ≥ 0
2x² - 5x + 2 ≥ 0
Д = (-5)² - 4 • 2 • 2 = 9
х_1;2 = (5±3)/4 = 2; 0,5

х є (-∞; 0,5) U (2; +∞);

6) 4х(х + 2) < 5
4x² + 8x - 5 < 0
Д = 8² - 4 • 4 • (-5) = 64 + 80 = 144
х_1;2 = (-8±12)/8 = -2,5; 0,5

х є (-2,5; 0,5).